PH380-Cours1

# Rappels de deuxième année

## Charge électrique $Q$

单位 : Coulomb, C

$e=1.6\times 10^{-19}\ \mathrm {C}$

## Champ électrique $\vec E$

向量场(champ vectoriel)

单位：$\rm V\cdot m^{-1}$

点电荷$q$在电场$\vec E$中受到电场力$\vec F=q\vec E$

点电荷$M(Q)$在$P$点创造出的电场强度：$\vec{E}(P)=\dfrac{Q}{4\pi\varepsilon_{0}||\overrightarrow{MP}||^{2}}\vec{u}$

## Potentiel electrique $V$

$\vec E = -\overrightarrow{\rm grad}\ V$ (cas statique)

## Densité volumique de courant $\vec j$

导体中电荷密度为$\mu$个/$m^3$，没，每个电荷电荷量为$q$，电荷柱行进速度$\vec v$，

则有$\vec j = \mu q \vec v$

单位：$\rm A\cdot m^{-2}$

宏观电流$I = \iint _S \vec j \cdot \mathrm d \vec S$

## Densité volumique de charge $\rho$

$\rho = \mu q$

导体中单位体积中自由电荷量为$\rho$，则$\vec j = \rho v$。

## Champ magnétique $\vec B$

单位：Tesla(T)

M点一段小电流$\vec j \mathrm d V$会在P点创造磁场：

$\mathrm d \vec B (P) = \dfrac{\mu_0}{4\pi}\left(\vec j \mathrm d V\right)\wedge \dfrac{\overrightarrow{MP}}{||\overrightarrow {MP}||^3}$

$\mu_{0}=4\pi\cdot10^{-7}\ \mathrm{H}\cdot\mathrm{m}^{-1}$

## Théorèmes importants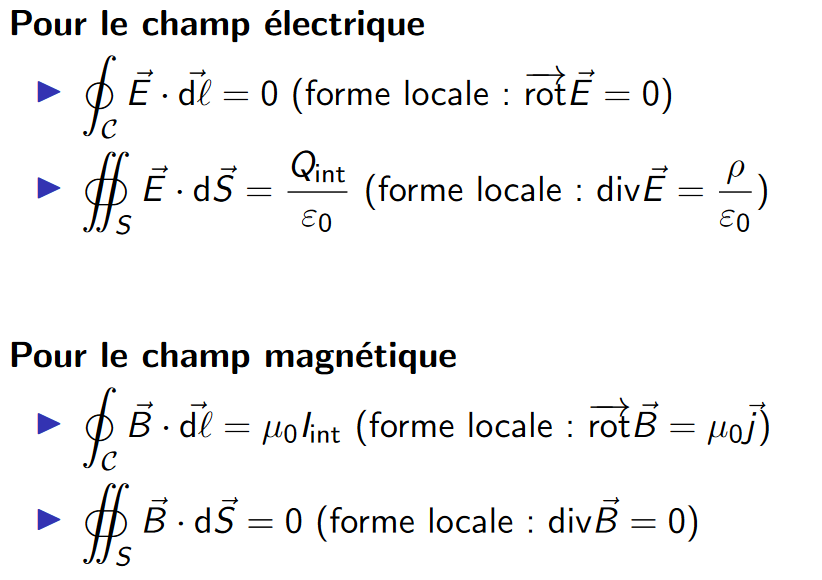

![](https://cdn.jsdelivr.net/gh/MapleWithered/img-storehouse@latest/picgo/img-2021-09-13-22-36-51.png)

## Force de Lorentz

点电荷q，速度v，放在E电场中，磁场B中，受到洛伦兹力F：

$\vec{F}=q\vec{E}+q\vec{V}\wedge\vec{B}$

## 解题方法

一般分析Symétries/invariances，然后再用Thm de Gauss/Ampère。

最后修改：2021 年 09 月 13 日

如果觉得这篇文章对你有用，请随意赞赏~